April 4, 2021 kotlin ingenieria de software
El algoritmo de Huffman fué desarrollado por David A. Huffman en 1952 y es la base de la compresión de archivos de texto como ZIP.
Antes de empezar, recordemos algunos conceptos básicos:
- Las computadoras entienden pulsos eléctricos representados por 1 y 0
- Cada letra de nuestro abecedario es representado por un conjunto de 8 bits, es decir, cada letra ocupa un espacio en nuestro disco duro de 1 Byte.
- La letra A es representada en la tabla ASCII por el número 65, en binario esto es,01000001
Ahora supongamos la siguiente cadena de caracteres,
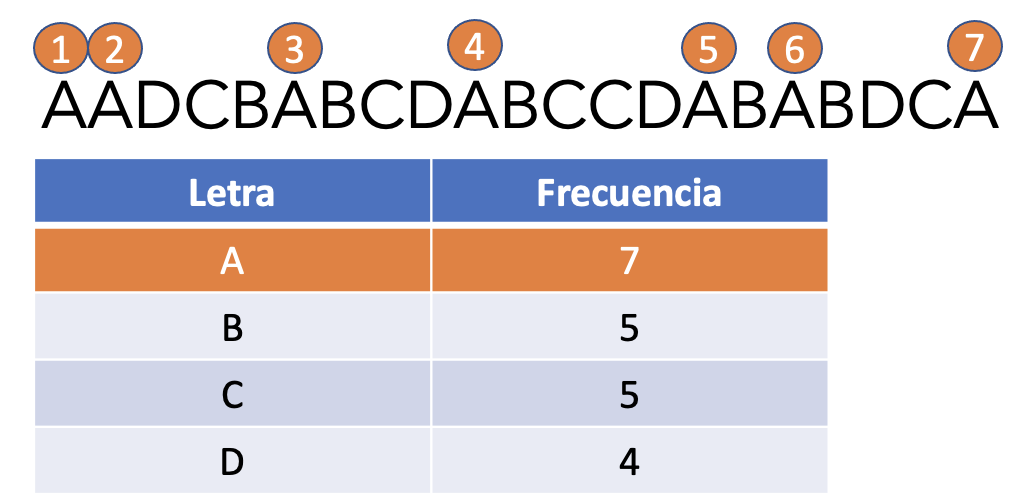
AADCBABCDABCCDABABDCA
Se trata de una cadena de 21 letras, por lo tanto nuestro archivo de texto pesaría 21 Bytes (más 1 byte de metadatos del archivo) ya que cada letra es 1 byte. La siguiente imagen ilustra esta explicación.
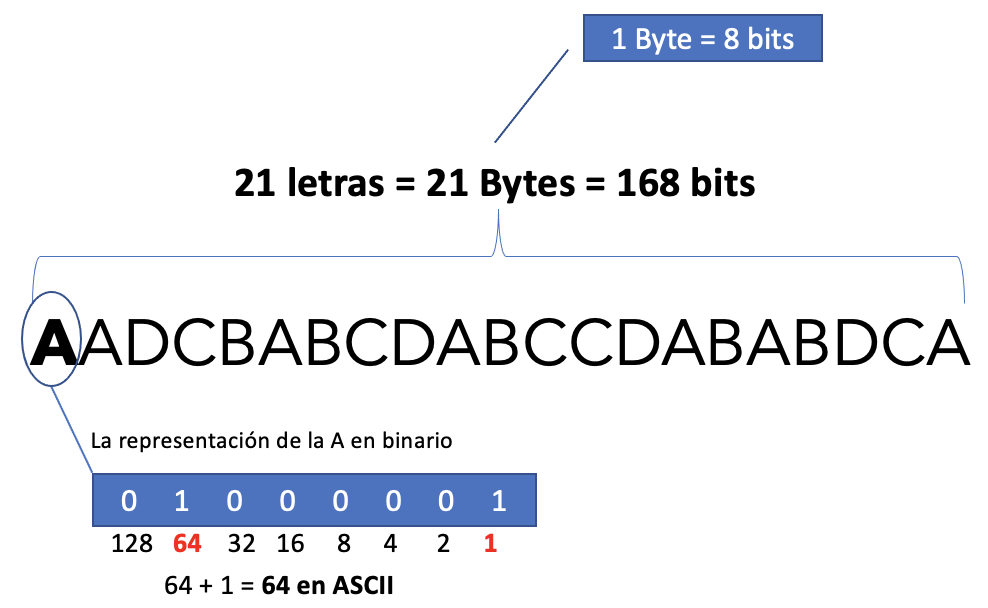
Dado que ya dijimos que las computadoras solo entienden ceros y unos, la representación binaria de la cadena anterior es esta:
010000010100000101000100010000110100001001000001010000100100001101000100010000010100001001000011010000110100010001000001010000100100000101000010010001000100001101000001
Lo anterior es lo que realmente contiene el archivo de texto.
Podemos crear un archivo de texto con la cadena anterior como contenido, luego ver el contenido binario del archivo mediante el comando xxd y validar que en efecto nuestro archivo pesa 22 bytes.
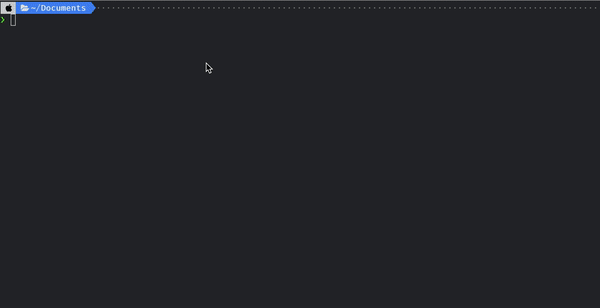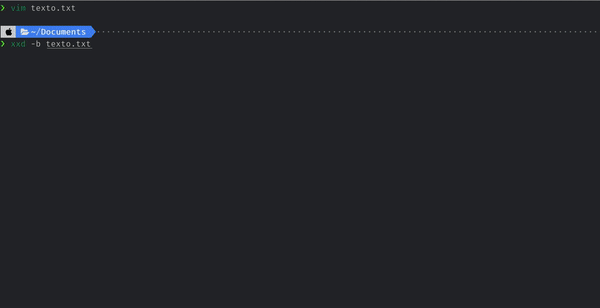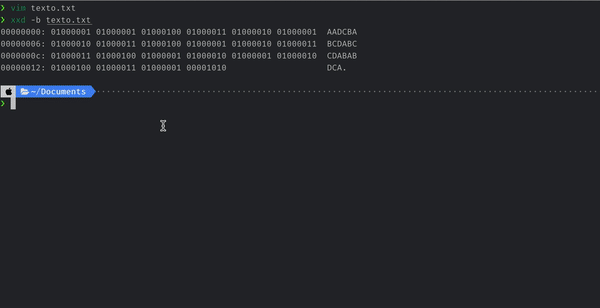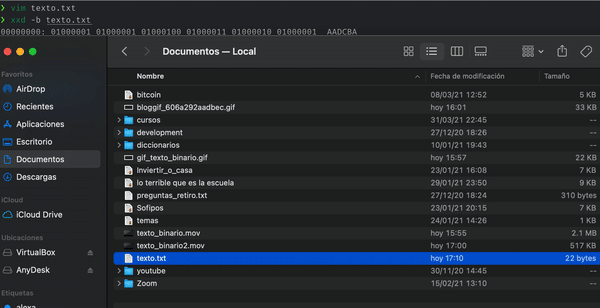
Construyendo un árbol binario
Lo primero que debemos hacer es calcular la frecuencia con la que aparece cada letra, por ejemplo, la letra ‘A’ se repite 7 veces, la ‘B’ y ‘C’ se repite 5 veces y por último la letra ‘D’ se repite 4 veces.
Ya sabemos que cada letra es representada por una serie de 8 bits
Ahora vamos construir un árbol binario que nos permita “crear una ruta” para acceder a cada una de las palabras de nuestra cadena, para ello nuestro árbol tendrá una raíz y a partir de ahí derivaremos 2 ramas, las ramas de la izquierda tendrán siempre el valor de cero y las ramas de la derecha el valor de 1. Siempre vamos a colocar en las ramas de la derecha la palabra con mayor frecuencia de repetición, en este caso, la letra ‘A’ es la que se repite más veces, por lo tanto la primer aproximación de nuestro árbol es la siguiente:
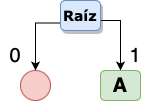
RECUERDA en las ramas de la izquierda va un cero y en las de la derecha vale 1 y se coloca la letra con mayor frecuencia de repetición.
A partir de aquí esto será un proceso iterativo, donde siempre tomaremos el nodo izquierdo para derivar 2 ramas más y colocar en la rama de la derecha la siguiente letra con mayor frecuencia, por lo tanto nuestra segunda aproximación del árbol binario es esta:
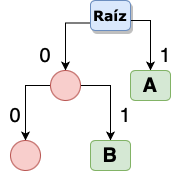
Podemos observar que tanto la letra ‘B’ y ‘C’ tienen la misma frecuencia de repetición 5, en este caso no importa si primero colocamos ‘B’ y después ‘C’ o viceverza. Repetimos los mismos pasos con el resto de las letras y finalmente tenemos el árbol final resultante:
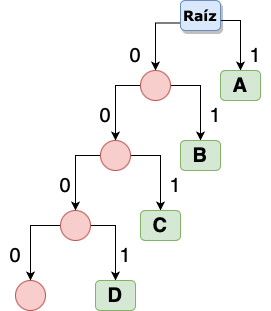
Recorriendo el árbol
Ahora que ya tenemos construido nuestro árbol, podemos recorrerlo para buscar una letra, por ejemplo, si queremos encontrar a la letra ‘C’ tendríamos que hacer el siguiente recorrido marcado en color rojo:
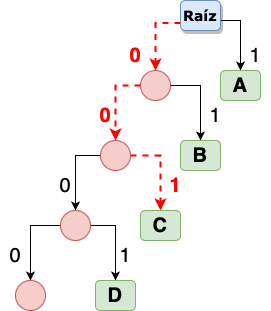
Por lo tanto, la letra C estará representada solo por 3 bits y no por 8 bits. Los bits que representan a ‘C’ son 001, resultado de recorrer nuestro árbol para llegar a ella. Para la letra ‘A’ solo hace falta hacer un simple recorrido y obtendremos 1 como su representación binaria, es decir, redujimos de 8 bits a 1 bit para representar a la letra ‘A’.
La representación binaria del resto de letras es la siguiente:
| Letra | Frecuencia | Representación |
|---|---|---|
| A | 7 | 1 |
| B | 5 | 01 |
| C | 5 | 001 |
| D | 4 | 0001 |
Una nueva representación binaria
Recordemos nuestra cadena de caracteres original:
AADCBABCDABCCDABABDCA
Mencionamos que su representación original en binario es la siguiente:
010000010100000101000100010000110100001001000001010000100100001101000100010000010100001001000011010000110100010001000001010000100100000101000010010001000100001101000001
Si aún no te has dado cuenta, el número binario anterior, no es más que la representación ASCII pero en binario, es decir, según la tabla ASCII la letra A está dada por el valor 65 en decimal, la B por el 66, C por el 67 y D por el 68
| Binario | Dec | Hex | Letra |
|---|---|---|---|
| 0100 0001 | 65 | 41 | A |
| 0100 0010 | 66 | 42 | B |
| 0100 0011 | 67 | 43 | C |
| 0100 0100 | 68 | 44 | D |
Sin embargo, ahora con la nueva representación, resultado de nuestro árbol binario, nuestra cadena de bits queda reducida así:
110001001011010010001101001001000110110100010011

Hemos pasado de tener 168 bits a solo 48 bits (cuenta cada cero y uno).
Ejercicio
Como ejercicio, puedes comprimir el siguiente texto usando el algoritmo visto:
Pase lo que pase, no te detengas
La representación en binario sería:
0101000001100001011100110110010100100000011011000110111100100000011100010111010101100101001000000111000001100001011100110110010100101100001000000110111001101111001000000111010001100101001000000110010001100101011101000110010101101110011001110110000101110011
Misma que puedes comprobar en la siguiente página
El texto comprimido te debería resultar en la siguiente salida binaria:
00000000000000100010010110000000000000100000011000000000000100000000000101100000000001000100101000000000110000010000001100001011000000001010000101000001000000010001001
¿Qué sigue?
En un próximo artículo, publicaré la implementación en kotlin de este sencillo algoritmo.
Con esto nos podemos dar una idea sobre como funcionan los algoritmos de compresión como el ZIP, adicional, el algoritmo de Huffman también se usa para imagenes como PNG, compresión de audio y video, etc. Como pudimos observar, la base del algoritmo es identificar la frecuencia con la que aparece una palabra. Para la compresión de sonido o imagen es similar, por ejemplo en imagenes PNG se buscan áreas rectangulares identicas, por ejemplo en una imagen con un fondo, dicho fondo es una repetición de bits que pasan por un proceso similar al descrito en este articulo.
